Proyecto Unidad 4: Visualizando el COVID-19

Al finalizar el proyecto, tu código deberá de ser capaz de replicar las siguientes imágenes:

Código Inicial

Descarga los archivos necesarios para comenzar este proyecto.

Inspiración

En proyectos anteriores hemos trabajado con modelos epidemiológicos, datos reales de contagios en nuestro país y estadísticas sobre los cambios en tendencias de movilidad. Todo esto lo hemos trabajdo simplemente en códigos, desplegando números, arreglos y DataFrames, sin embargo en muchas ocasiones para que el ser humano puede identificar patrones, reconocer comportamientos o simplemente visualizar de forma más amena la información utiliza gráficas.

Por ejemplo, cuando se hace una presentación sobre un tema, generalmente se muestran los gráficos obtenidos a partir de esos datos, no simplemente los valores ordenados en tablas. Otro ejemplo es con las conferencias sobre la pandemia en nuestro país, la forma en que representan estos datos es a través de gráficas de barras, no tablas de datos.

Siendo así, ahora es turno de convertir nuestros proyectos anteriores en algo más cercano a nosotros, las tablas son muy buenas para las computadoras, las gráficas son mejores para los humanos.

Recordarás que, en el proyecto de la Unidad 3 trabajamos con los conjuntos de datos de movilidad de Google, así como los números de la pandemia brindados por el Gobierno de México. Ahora es turno de sacar provecho de ese DataFrame que creaste y entender las afectaciones o beneficios que han tenido los cambios de movilidad en los diferentes estado de nuestro país. Antes de eso, tal vez sea buena idea ver primero los comportamientos de movilidad, ya que hacerlo en un DataFrame de cientos de filas no es tarea fácil, pero una gráfica puede decirnos mucho más.

Por otra parte, recordarás el modelo SIR que trabajaste en el proyecto de la Unidad 2, donde trabajamos con un arreglo de personas y simulábamos un proceso epidemiológico. Vamos a retomar ese modelo también aquí, pero de una forma más rigurosa matemáticamente.

Recordarás que anteriormente simulábamos por días, un día a la vez. Este proceso se conoce como discreto lo que quiere decir que vamos a pasos enteros, por ejemplo de uno en uno los días. Sin embargo, podrás decir, y con toda la razón, que no es así como funcionan en la realidad. Resulta que estos procesos son un continuo ya que en ningún momento se detienen. Además, recordarás que habíamos impuesto una forma cuadrada para la distribución de nuestra población, así como que los individuos fueran estáticos y únicamente pudieran estar en contacto con los de sus alrededores. Bien, pues para librarnos de estas restricciones forzadas vamos a definir el modelo SIR como una ecuación diferencial (un proceso continuo, que dicta los cambios de una variable con respecto a otra).

Para los susceptibles tenemos la siguiente ecuación: $$\frac{dS}{dt}=-\beta \frac{IS}{N}$$ Podemos entender la ecuación si analizamos por partes el lado derecho.

Cada infectado tiene una probabilidad $\frac{1}{N}$ de interactuar con un susceptible. Si tenemos S susceptibles, obtenemos entonces el término $\frac{S}{N}$ .

Ahora, cada infectado tiene dicha probabilidad de interactuar con un susceptible, por tanto se obtiene $$I\frac{S}{N}$$ que es el término que define la proporción de infectados que interactúan con susceptibles.

Recordemos también que la tasa o probabilidad de que en una interacción entre infectado y susceptible haya contagio está regulada por el factor β, de ahí obtenemos que por cada interacción entre susceptibles e infectados se tiene la probabilidad β de que el susceptible se infecte y por tanto queda la ecuación siguiente $$\beta \frac{IS}{N}$$

Finalmente, al ser el cambio de susceptibles en el tiempo, el valor debe de ser negativo puesto que si un susceptible se infecta, pasa al estado de infectado, y por tanto reduce el número de personas susceptibles. Lo que nos queda modelado en la ecuación diferencial $$\frac{dS}{dt}=-\beta \frac{IS}{N}$$ que nos indica que el cambio de susceptibles en el tiempo (parte izquierda de la ecuación) está dado por la probabilidad β de que en una interacción entre infectado y susceptible, el segundo quede infectado.

Ahora veamos el caso de los removidos. Para este estado la ecuación diferencial luce de la forma siguiente $$\frac{dR}{dt}=\gamma I$$

De nueva cuenta, si analizamos la parte derecha de la ecuación podemos enteder lo que nos dice. I es el número de infectados, y recordando que γ es la tasa o probabilidad de que un infectado se recupere o muera, entonces podemos entender que para cada infectado se calcula la probabilidad de que sea removido y entonces pasa a ese estado. Por tanto tenemos que el número de removidos en el tiempo aumenta conforme los infectados se recuperan a una tasa γ

Por último tenemos la ecuación de los infectados que luce como sigue $$\frac{dI}{dt}=\beta \frac{IS}{N}-\gamma I$$

El lado derecho de esta ecuación contiene dos términos: el primero corresponde con los nuevos casos infectados y corresponde con el lado derecho de la ecuación de los susceptibles, pero de signo positivo, esto quiere decir que se agregan los nuevos infectados que pasaron del estado susceptible. El segundo término es la tasa a la que los infectados pasan al estado de removidos, e igualmente corresponde con el lado derecho de la ecuación pero ahora de los removidos, pero con signo negativo ya que con cada nuevo removido se reduce el número de infectados.

De forma que nuestro sistema de ecuaciones diferenciales queda descrito de la forma siguiente para el cambio en el tiempo de los susceptibles $$\frac{dS}{dt}=-\beta \frac{IS}{N}$$ los infectados $$\frac{dI}{dt}=\beta \frac{IS}{N}-\gamma I$$ y los removidos $$\frac{dR}{dt}=\gamma I$$ este conjunto de ecuaciones nos permiten modelar de mejor manera un fenómeno epidemiológico en una población.

Proyecto

En este proyecto desarrollarás dos códigos independientes que deberán de exportar dos imágenes cada uno.

Uno de ellos deberá simular un modelo SIR a través del sistema de ecuaciones diferenciales antes mencionado, y al finalizar graficará los valores de cada estado en el tiempo en una misma imagen. Además, con esos resultados deberá de calcular el número de casos diarios en la simulación y hará un histograma con ellos.

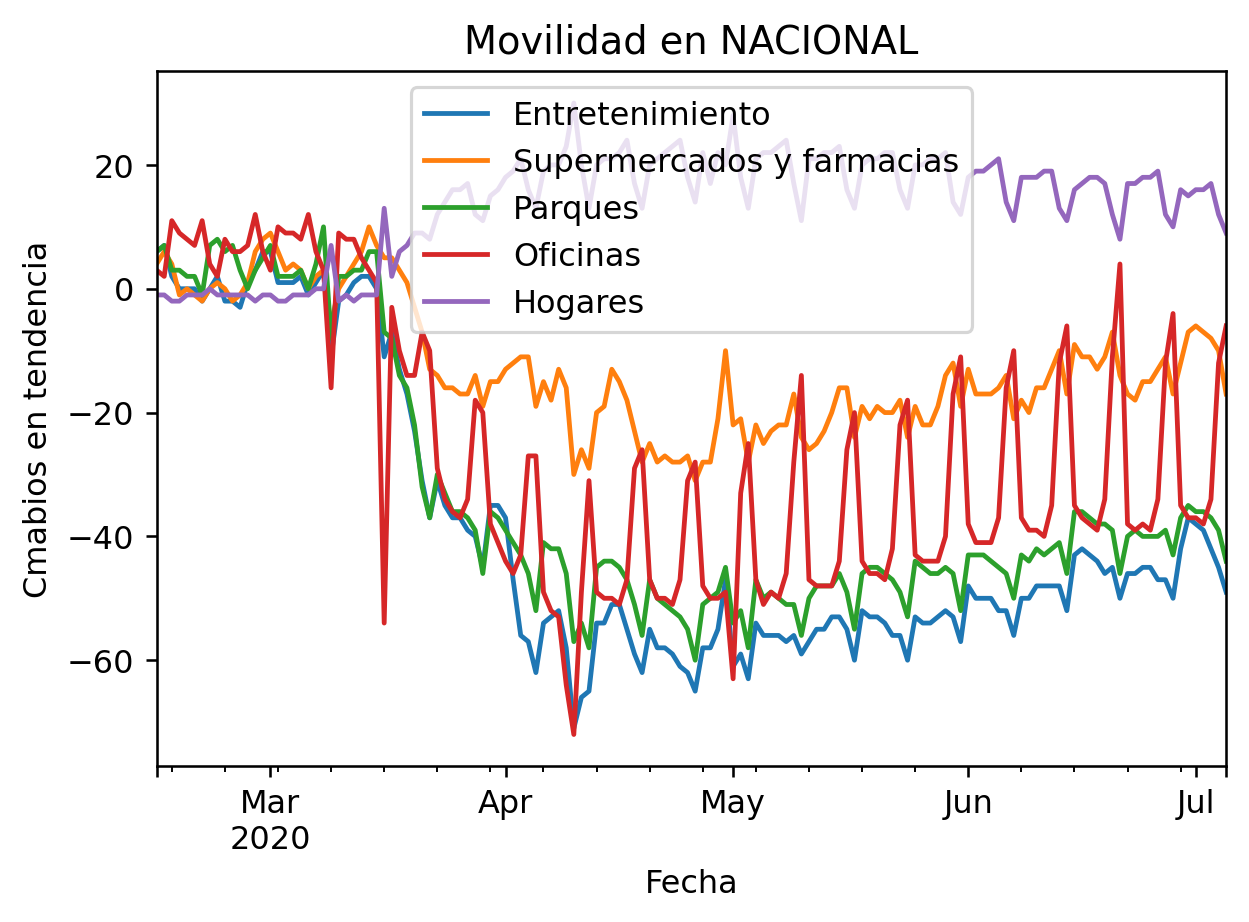
El otro código tendrá que leer el archivo .csv con el DataFrame que contiene tanto los datos de movilidad como los números de la pandemia en México (recuerda que ese DataFrame ya lo hiciste en tu proyecto pasado, así que no debe de haber mayor problema para la lectura). Una vez que tengas los datos, harás un gráfico mostrando todos los cambios de tendencia de movilidad de un estado en particular (lo dejamos a tu elección) a lo largo del tiempo. 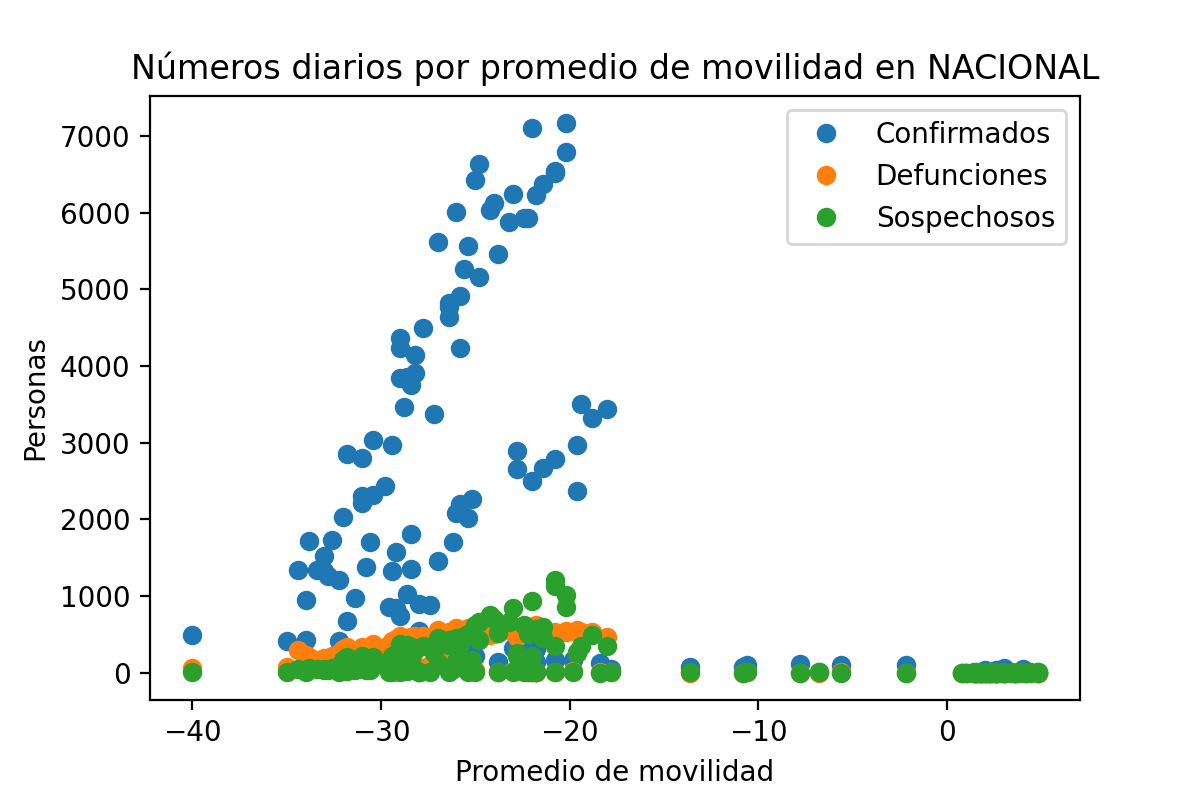Igualmente crearás otro gráfico diferente donde coloques en el eje x el promedio de las tendencias de movilidad en un día, y en el eje y sus respectivos números (confirmados, defunciones y sospechosos), este será un gráfico de dispersión (también llamado scatter plot).

Considera en todas las gráficas añadir los nombres de los ejes, las leyendas de lo que estás graficando así como el título que mejor describa los datos graficados.

Ayudas

En la carpeta comprimida (.zip) que descargaste al principio de esta página encontrarás dos códigos que serán los que ocupes para llevar a cabo tu proyecto.

ModeloSIR.py

Este script contiene una sección de código ya implementada para tí. En ella importamos toda la paquetería de numpy así como la función odeint del paquete scipy, la cual funciona como un solucionador de ecuaciones diferenciales.

Para solucionar una ecuación diferencial en Python se necesitan tres cosas:

• Modelo de ecuaciones diferenciales como una función
• Condiciones iniciales
• Tiempo de solución

En el código en ModeloSIR.py el modelo está definido en la función sir que toma como argumentos y que representa los valores del modelo, t el tiempo en la simulación y beta y gamma son los parámetros de nuestro modelo (β y γ). Sin embargo, además de los estados S, I y R, agregamos C, que va a llevar al cuenta de los infectados acumulados a lo largo del tiempo.

En esta función se descompone y en los valores de S, I, R y C. Una vez que se tienen, sumamos S, I y R para conocer el valor total de la población N. Con esto ya tenemos todos los valores necesarios para el modelo.

De forma que calculamos los valores de los dos términos que hay en nuestra ecuación de la siguiente manera:

• infectados=beta*I*S/N que es el equivalente a $\beta \frac{IS}{N}$
• removidos = gamma*I que equivale a $\gamma I$

Una vez que contamos con estos términos, los acomodamos y les ponemos el signo correspondiente según el modelo SIR, quedando de esta forma dydt el vector con las derivadas como [-infectados, infectados-removidos, removidos, infectados]. Con eso queda completa la implementación de las ecuaciones diferenciales en una función.

Después, como toda ecuación diferencial, para poder resolverla es necesario contar con el conjunto de condiciones iniciales. En nuestro modelo SIR significa cuántos susceptibles, infectados, removidos e infectados acumulados iniciales hay.

Antes de elegir los valores, es necesario que definamos un tamaño de población. Asignamos la variable población con esa intención. De inicio le hemos dado un valor de 100, pero siéntete libre de modificarlo a tu gusto.

Ahora que ya tenemos una población finita, podemos darle valores a las condiciones iniiciales de nuestro modelo. Podrás observar que deifinimos I0 como el número inicial de casos, y lo hemos asignado al valor poblacion * 0.01 por darle un valor, pero puedes cambiarlo a tu gusto.

Una vez teniendo esos dos valores construimos nuestro arreglo de condiciones iniciales y0 inicializado con [poblacion - I0, I0, 0, I0], donde el primer valor son los susceptibles iniciales, el segundo los infectados iniciales, posteriormente los removidos iniciales y finalmente los infectados acumulados, contemplando los iniciales.

Finalmente definimos t como los tiempos en los que se va a solucionar el sistema de ecuaciones, como lo hemos asignado es una sucesión de números del 0 al 40 en pasos de uno en uno, para que cada uno representen un día.

Ya contando con todo lo anterior podemos resolver nuetsro modelo, para ello utilizamos odeint que recibe como argumentos sir el modelo, y0 que son las condiciones iniciales, t los tiempos de solución y como argumentos adicionales pasamos la tupla (beta, gamma) que son los parámetros de nuestro modelo. Esta función nos regresa un arreglo con la solución de cada una de las variables del modelo en los tiempos de simulación marcados en t. Por ejemplo, para acceder a los valores de susceptibles en el tiempo utilizamos la notación para arreglos de dos dimensiones sol[:, 0] siendo sol el arreglo regresado por odeint.

VisualizacionMovilidad.py

En este código tú tendrás que hacer la implementación. Únicamente hemos importado los paquetes de pandas y matplotlib.pyplot que consideramos te serán de ayuda para la implementación.

Especificación

Para llevar a cabo este proyecto deberás de implementar ambos códigos.

En VisualizacionMovilidad.py debéras de lograr lo siguiente:

• Leer el archivo .csv con todos los datos.
• Elegir uno de los estados (e.g. QUERETARO) y seleccionar de entre todos los datos únicamente los que le corresponden. Tal vez te sea de utilidad el método unique de pandas para ver los diferentes estados que hay en el DataFrame.
• Con los datos seleccionados podrás llevar a cabo la gráfica de movilidad. A esta le tendrás que agregar nombres a los ejes y su respectivo título.
• Posteriormente tendrás que hacer un promedio de las tendencias de movilidad por día. Para ello puede que encuentres de utilidad la función mean de pandas y presta atención en los argumentos que se le pueden pasar, recuerda que queremos hacer un promedio por fila, no por columna.
• Ya que tengas los promedios de movilidad por día, podrás graficarlos contra el número de casos confirmados, defunciones y sospechosos en las mismas fechas, de forma que puedas observar si existe algún tipo de tendencia o impacto de uno sobre otro. Por último recuerda agregar leyendas, título y ejes.

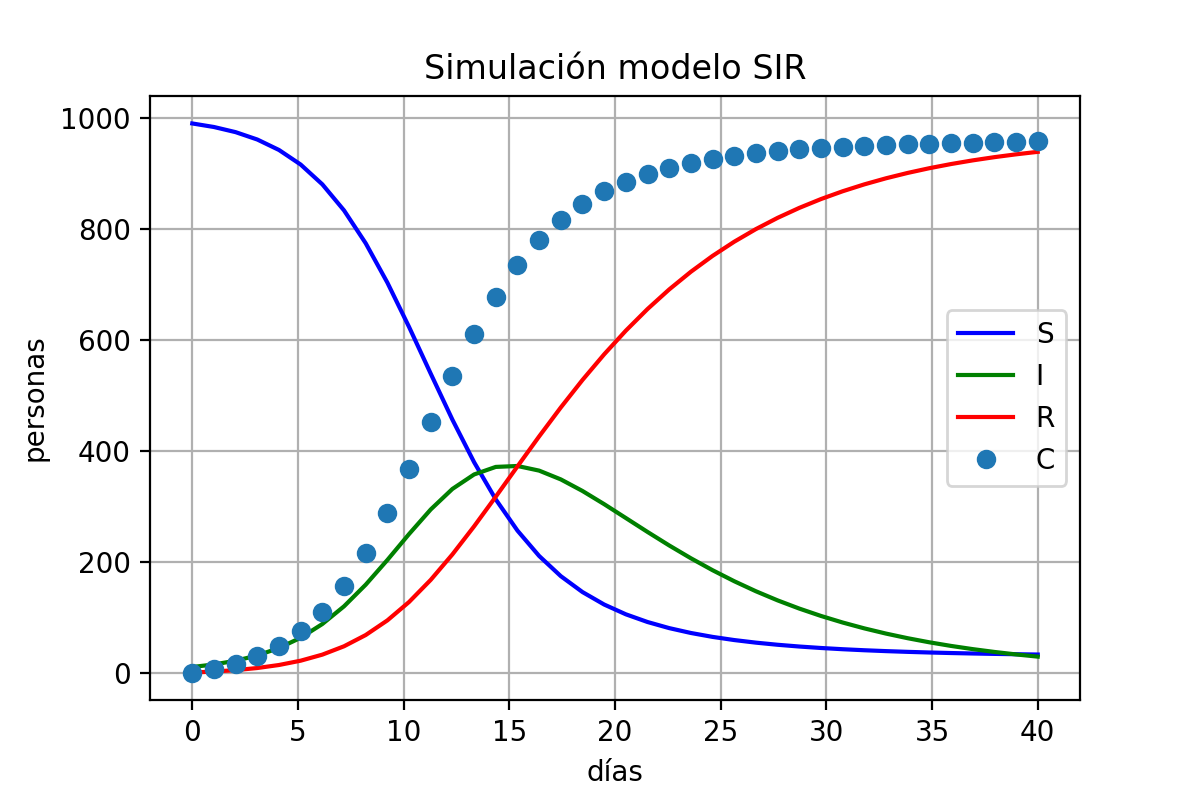
Para ModeloSIR.py deberás de graficar las series de tiempo de cada uno de los diferentes estados del modelo, los cuales se encuentran en sol. Este gráfico deberá de contar con todos los esatdos en sol, cada una con su respectiva leyenda, así como los nombres en los ejes y título.

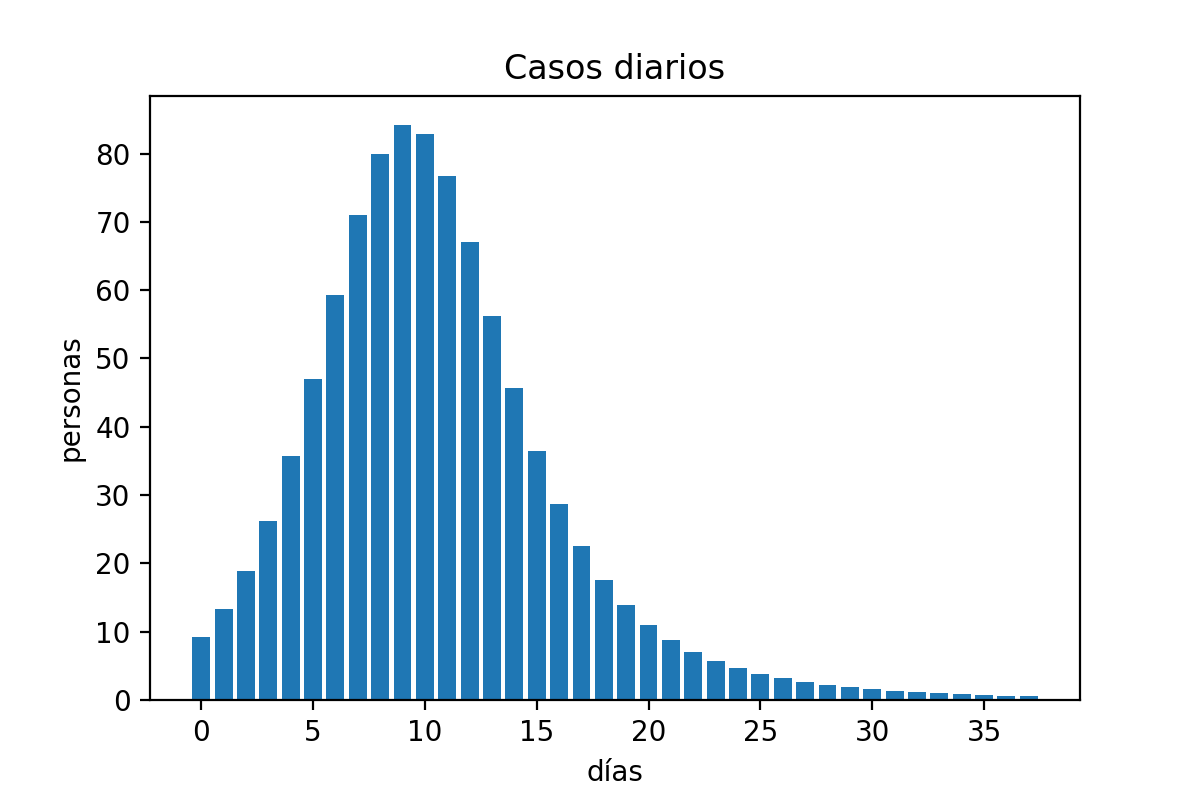
Ya que cuentes con la gráfica de los tres estados, tendrás que hacer el histograma de casos diarios. Este número no está en el modelo, sino que debes de calcularlo con los datos que sí tienes de la simulación. La forma de obtenerlos es a atrvés de acumulados, ya que la diferencia entre un día y el otro es el número de casos confirmados en esa fecha. Ya que tengas el arreglo con los datos, podrás hacer el histograma y agregarle sus ejes y título como a las anteriores gráficas.

Walkthrough

Este proyecto tiene dos vídeos de apoyo, asegúrate de ver ambos. El segundo vídeo se cargará automáticamente al acabar el primero, o puedes utilizar los botones de siguiente y anterior para pasar de uno a otro.

Resultados esperados

Al final, tus códigos deberán de ser capaces de generar las figuras que muestren el comportamiento de la simulación con el modelo SIR, tanto de los estados S, I, R y C a lor largo del tiempo, así como el histograma con los casos diarios.

Si tienes curiosidad, modifica el código que hiciste en el proyecto de la Unidad 2 para que puedas guardar en cada paso de simulación los valores de los estados S, I y R. Una vez que los tengas, grafícalos. ¿Qué tan parecidos son con los del modelo de ecuaciones diferenciales? ¿Probaste con parámetros iguales? ¿Qué diferencias notas entre los gráficos? ¿Crees que representa el mismo fenómeno epidemiológico?

Por otro lado, para la visualización de datos de movilidad, al final del proyecto tu código deberá de ser capaz de graficar todos los valores de cada tendencia de movilidad como una serie en el tiempo.

También podrás comparar los números de la actual pandemia y confrontarlos contra la movilidad de cada región. ¿Qué tanto cambian los resultados entre estados? ¿Crees que promediar las tendencias de movilidad es lo suficientemente expresivo para entender el fenómeno? ¿Qué tal si la afectación de la movilidad sobre los números no es el mismo día, sino días depués? Si te sientes con la suficiente seguridad, intenta responder algunas de estas preguntas a partir de modificar y gráficar los datos, ¿qué podrás encontrar?

Si todavía no cuentas con el conjunto de datos del proyecto 3, aquí podrás descargar el archivo como debe de quedar al final del proyecto. Considera que esto no equivale a ya no hacer el proyecto 3, sino que te brindamos los datos para que puedas hacer el proyecto 4 sin depender del anterior.

Solución al proyecto

Archivos con la solución al proyecto Visualizando el COVID-19.